CSAPP: Data Lab

Posted on Edited on In

Some Restriction

又复习了一次位级表示

Integer Coding Rules

  1. Expr
    1. 整型操作数的值被限制在范围[0, 255]。
    2. 不能使用全局变量
    3. 只能使用的一元操作!, ~
    4. 只能使用的二元操作&, ^, |, +, <<, >>
    5. 一个表达式不会被限制拥有多个操作符
  2. Fobidden
    1. 使用控制语句如if, do, while, for, switch等等
    2. 定义或使用任何宏
    3. 在当前文件中定义任何额外的函数
    4. 调用任何函数
    5. 使用其他操作
    6. 使用类型转换
    7. 使用除int之外的任何数据类型，使用arrays, structs, unions
  3. 假设机器的配置
    1. 使用2的补码，int的表示为32-bit
    2. 执行算术右移
    3. 如果左移的位数小于0或者大于31则会出现未预测的行为。

Floating Point Coding Rules

  1. Forbidden
    1. 定义或使用任何宏
    2. 定义任何额外的函数
    3. 调用任何函数
    4. 使用任何形式的类型转换
    5. 使用arrays, structs, unions

Notes

  1. 使用dlc(data tab checker)编译器来检查解决方案的合理性
  2. 使用btest来检查你的函数的正确性
  3. 使用BDD checker来正式地证实你的函数

lab Note

  1. 64位机器上编译32位程序会出现错误fatal error: bits/libc-header-start.h: 没有那个文件或目录，是因为gcc没有安装multilib库，这个库可以在64位的机器上产生32位的程序sudo apt install gcc-multilib

1. bitXor

通过图中所给的与、非和或门构造的异或逻辑电路，再利用德摩根定律将所有的或门转化为与门可得。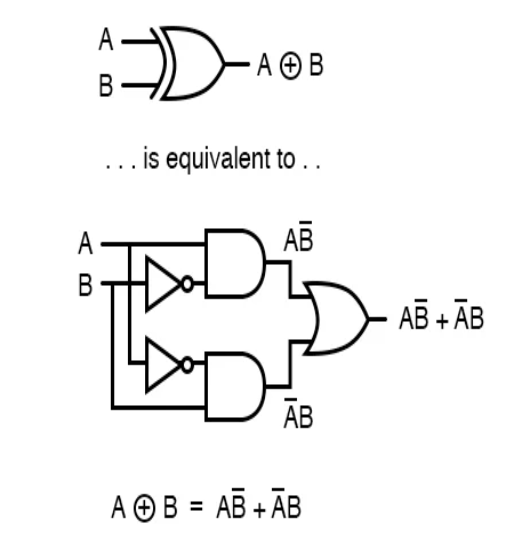
XOR gate

1
2
3
4
5
6
7
8
9
/* bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) { 
  return ~((~(x&(~y))) & (~((~x)&y)));
}

2. tmin

32位整型数2's complement的范围为[-2^(n-1), 2^(n-1)-1, 很容易得出结果

1
2
3
4
5
6
7
8
9
10
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 1 << 31;

}

3. isTmax

摸索了小一段时间，解法很多，-1可以通过取反+1来构造。假设x为Tmax, 对Tmax取反得到Tmin，再减1则会发生underflow会得到Tmax, 通过逻辑运算的结果与x本身异或，看结果是否为0来判断Tmax。这种情况下-1是需要排除的, 因为对-1的2's Complement取反得到0，减1之后会得到-1本身，因此异或结果还是0，需要排除(利用好!!,保证与的操作数要么是0或1)。排除直接让x+1判断即可，否则操作数会超出10个。

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  return (!(((~x)+(~1+1))^x)) & (!!(x+1));
}:

4. allOddBits

根据题目给定的操作符数的限制，以及操作数值的限定，即可确定需要利用好0xAA。同样也花了一些时间去斟酌，很多细节需要把握住，得到最终的答案。

1
2
3
4
5
6
7
8
9
10
11
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  return !((((x&0xAA)&((x>>8)&0xAA))&(((x>>16)&0xAA)&((x>>24)&0xAA)))^0xAA);
}

5. negate

很简单

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x+1;
}

6. isAsciiDigit

可以先将操作数限定在0x3X的范围内，再通过对0x0A取补得到-10，取低4位进行加法运算，得到的结果通过符号位，若符号位为1则为ASCII数字，否则不满足条件。可以通过提取从低位数起第五个bit即0x10来确定符号位。

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  int neg_A = ~0x0A+1;
  return ((!((x>>4)^0x3)) & (!!(((x&0xF)+neg_A)&(0x10))));
}

7. conditional

保证x非0即1，再利用0和1补码的特点, 构造全1和全0, 分别和y, z完成与运算来进行排除，这道题还是非常巧妙的。

1
2
3
4
5
6
7
8
9
10
11
/* 
 * conditional - same as x ? y : z
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) { 
  int mask = ~(!!(x^0x0))+1; 
  return (y&mask) + (z&(~mask));
}

8. isLessOrEqual

根据两个参数x, y的符号位先分几种情况

  1. 满足小于等于
    1. 两数相等
    2. x<0, y>0, 避免符号位相等时的溢出情况
    3. 符号位相等比较。通过第一个操作数加上第二个操作数的取补的形式, 若结果小于0，则x<y
      • 负负比较, 可能会出现对Tmin取补发生下溢出的特殊情况，因此需要排除第二个操作数为Tmin的情况，恰好该情况要么相等(已经判断过了), 要么就是x>y(也判断了)。
      • 正正比较
  2. 不满足小于等于,即大于等于(x>0, y<0)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    /* 
     * isLessOrEqual - if x <= y  then return 1, else return 0 
     *   Example: isLessOrEqual(4,5) = 1.
     *   Legal ops: ! ~ & ^ | + << >>
     *   Max ops: 24
     *   Rating: 3
     */
    int isLessOrEqual(int x, int y) {
      int x_sign_bit = ((x>>31)&0x01);
      int y_sign_bit = ((y>>31)&0x01);
      int Tmin = 1 << 31;
      return (!((~x_sign_bit)&y_sign_bit)) & ((!(x^y)) | (x_sign_bit&(~y_sign_bit)) | ((((x+(~y+1))>>31)&0x1)&(!!(y^Tmin))));
    }

9. logicalNeg

首先要将想一个办法将0和正数，负数区分开来。因为0和正数的符号位都是0，要区分开来恰好利用到了0的补码还是其本身的特性，正数取反加一后符号位由0变1，可以直接区分开来。再利用算数右移的特性，将0构造成全0，负数和正数构造成全1, 最后+1得到返回值。

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4
 */
int logicalNeg(int x) {
  return ((x>>31)|((~x+1)>>31))+1;
}

10. howManyBits

坦白说这一题真的是卡了我好久，即便找到了最高bit位要想返回正确的结果几乎是很繁琐的，但肯定会超出操作符的限制。这道题参考了一下各路佬的思想，可以用二分法来实现。还需要注意负数需要按位取反(排除符号位的影响)，正数保持不变即可，可以通过sign_bit减1来构造全0和全1。可以通过右移16、8、4、2、1bit来找到最高的bit 1，这道题还是非常巧妙的。
判断右移n bit后是否为0

  • 如果为0，说明需要的位在高n-bit(左半侧)，数则保持不变，故不记录n，继续进行二分搜索。
  • 如果不为0，说明需要的位在低n-bit(右半侧), 数向右移动n-bit继续进行搜索，且记录n。
    最后将所有移位得到的n都累加起来得到最后的结果
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    /* howManyBits  - return the minimum number of bits required to represent x in
     *             two's complement
     *  Examples: howManyBits(12) = 5
     *            howManyBits(298) = 10
     *            howManyBits(-5) = 4
     *            howManyBits(0)  = 1
     *            howManyBits(-1) = 1
     *            howManyBits(0x80000000) = 32
     *  Legal ops: ! ~ & ^ | + << >>
     *  Max ops: 90
     *  Rating: 4
     */
    int howManyBits(int x) {
      int b16, b8, b4, b2, b1, b0;
      int sign_bit = (x>>31)&0x1;
      int flag = sign_bit+(~1+1);   // neg -> all 0,  not_neg -> all 1
      x = ((~flag)&(~x))|(flag&x);  // if neg, reverse.
      b16 = (!!(x>>16))<<4;
      x >>= b16;
      b8 = (!!(x>>8))<<3;
      x >>= b8;
      b4 = (!!(x>>4))<<2;
      x >>= b4;
      b2 = (!!(x>>2))<<1;
      x >>= b2;
      b1 = !!(x>>1);
      x >>= b1;
      b0 = x;
      return b16 + b8 + b4 + b2 + b1 + b0 + 1;
    }

11. floatScale2

描述里没有给Infinity的case，通过测试发现，与Nan返回值一致合并一起判断。需要判断几种情况: NaN, Subnormal, +0, -0, Normalize。Normalize的情况只需要对Exponent的最低位增加一个bit即可。注意Subnormal情况Fraction为全1时左移的结果不需要将Exponent清零，按测试用例应该是将Subnormal转化为Normalize了。强调一下移码的意义为IEEE 754 Normalize表示部分2的指数部分。
$$Bias = 2^{Exponent-1}-1$$
$$Normalize = 1.Fraction \times 2^{Exponent + Bias} (1 \leq Exponent \leq 2^{Exponent} - 2)$$
$$Subnormal = 0.Fraction \times 2^{1-Bias}$$
$$Biased = Unsigned - Bias$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  int exp_mask = 0x7F800000;          // the eight bits of exponent is all 1.
  int Neg_zero = 0x80000000;
  int sign_mask = Neg_zero;
  int fraction_mask = 0x007FFFFF;
  if (!((uf & exp_mask)^exp_mask)) {       // eliminate the case of NaN.
    return uf;
  }
  if (!uf) {                     // eliminate the case of +0.
    return 0;
  }
  if (!(Neg_zero^uf)) {          // eliminate the case of -0.
    return Neg_zero;
  }
  if (!(uf & exp_mask)) {              // elinimate the case of subnormal.
    return (uf&sign_mask) + (((uf&fraction_mask)<<1));
  }
  uf += (0x1<<23);               // Normalize.
  return uf;
}

12. floatFloat2Int

实现到IEEE754单精度浮点数到定点整数的转换。题目中首先要考虑溢出的情况，早在最开始实验就假设机器左移的位数小于0或者大于31都会出现未知的行为，因此需要将这两种情况包含进去。由于Normalize的M部分是$1.Fraction$因此需要将小数点前面的1提前加入fraction部分。实际上fraction右移23位可以和$2^{Biased}$的指数部分进行相减$2^{Biased-23}$，进行对应的移位操作完成$2^n$幂次运算，最后得到对应的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  int bias = 1-(1<<7);
  int exp_mask = 0x7F800000;
  int fraction_mask = 0x007FFFFF;
  int fraction = (uf & fraction_mask);
  int exp = (uf & exp_mask) >> 23;
  int sign_bit = (uf>>31)&0x1;
  int biased = exp + bias;
  if (!(exp^exp_mask) || biased > 31) {  // NaN and infinity
    return 0x80000000u;
  }
  if (!uf || !(uf^0x80000000)) {
    return 0;
  }
  if (biased < 0) {
    return 0;    
  }
  fraction |= (1<<23);  // 1.F
  if (biased >= 23) {
    fraction <<= (biased-23);
  } else {
    fraction >>= (23-biased);
  }
  if (sign_bit)
    return -fraction;
  else
    return fraction;
}

13. floatPower2

给定argument为Biased，求出其对应无符号IEEE 754单精度浮点数的表示即可。求出exp的值之后，左移23到IEEE754规格的exponent域中。认真读题后还是蛮简单的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    int bias = 127;
    int exp = (x + bias)<<23;  // x = exp - bias
    int f = 0;
    if (x < -127) {              // too small(exp are all 0s that is Subnormal)
      return 0;
    } else if (x > (255-127)) {  // too large(the floating point number is larger than INF that exp are all 1s)
      return 0x7f800000;         // +INF
    }
    f |= exp;    // normalize
    return f;
}

运行结果

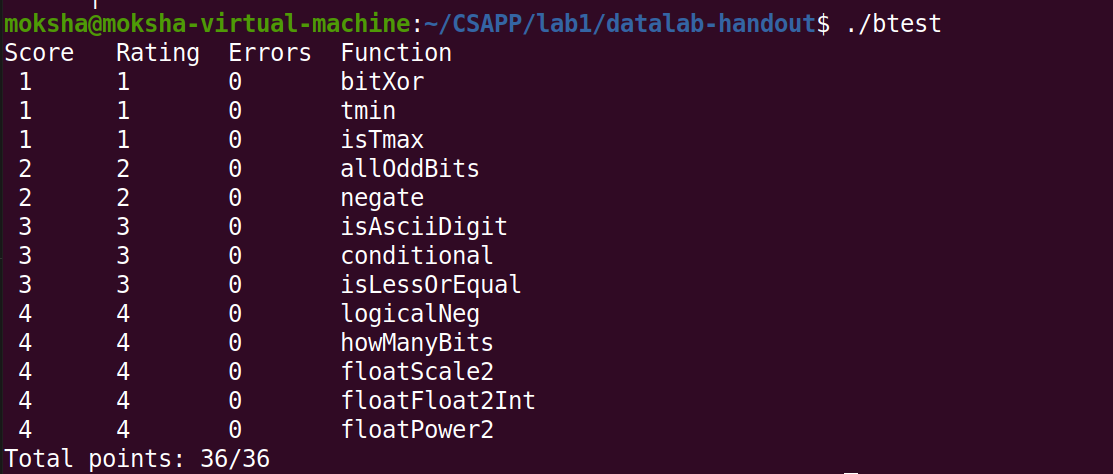
./btest
./dlc