CS61B Lec Note

Posted on 2022-05-18 In CS61B

Data Structure in Java

CS61B Data Structure Notes

Java Syntax

Java除了8种基本类型(按值传递)byte, short, int, long, float, double, boolean, char之外，其他一切，包括数组，不是原始类型，而是Reference Type(引用类型)，说白了就是指针。
声明任何引用类型(Reference Type)的变量，java会分配一个64-bit的box，这64-bit种不包含数据(如对象的属性等)，而是包含该数据的在内存中的地址。
1
2
3
Walrus a = new Walrus(1000, 8.3);
Walrus b;
b = a; // 将a在内存中的地址赋给b，使a和b指向同一内容。
嵌套类(Nested Class)。经验法则：如果不使用外部类的任何实例成员，则将嵌套类定义为static。因为被声明为static的嵌套类不能访问外部类的实例成员, 同时也节约了内存。
文件名必须和类名相同，每个文件必须只包含一个外部类。

泛型(Generic Type)仅适用于引用类型，尖括号内不能放入原始类型比如:int, double, 但是可以放入原始类型的引用版本，如: Integer, Double, Character, Boolean, Long, Short, Byte, Float。

public class DLList<genericTypeName> {
    public class IntNode {
        public IntNode prev;
        public genericTypeName item;
        public IntNode next;
        public IntNode(IntNode _prev, genericTypeName _item, IntNode _next) {
            this.prev = _prev;
            this.item = _item;
            this.next = _next;
        }
    }
    public DLList(genericTypeName x) {
        prev = new IntNode(null, x, null);
    }
    public static void main(String args[]) {
        DDList<String> d1 = new DLList<>("hello");
        DDList<Integer> d2 = new DDList<>(5);
        // 上一行代码和这行是相等的实例化尖括号声明类型可以省略
        DDList<Integer> d2 = new DDList<Integer>(5);
    }
}

创建数组的三种方法:

1
2
3

x = new int[3];
y = new int[]{1, 2, 3, 4, 5};
int[] z = {9, 10, 11, 12, 13};   // 类似第二种方法，但只能和声明结合时使用

java数组仅在运行时执行边界检查。System.arraycopy()方法非常方便使用。
[]允许我们在运行时指定想要的索引，而类中指定字段就不行。
创建泛型对象数组的方法(虽然java不允许，而且编译器会报错)
1
Glorp[] items = (Glorp []) new Object[8];
判断两个字符串是否相等使用equals而不是==的原因是，==比较的是地址，而equals比较的是存储单元中的值。
java不允许使用>运算符在字符串之间比较，而是用str1.compareTo(str2)来进行比较，如果相等则返回0，str1 > str2则返回一个正数。
org.junit库提供了很多方法来简化测试的编写, Junit官方文档; import static org.junit.Assert.* import org.junit.Test之后，就可以省略掉org.junit.Assert前缀，进而直接使用assertEquals方法; 需要在每个方法前加上@org.junit.Test来替代@Test, IDEA中Junit可视化测试是根据@Test标签在运行时自动检测的。
获取String的第i个字符的方法str.charAt(i)。
Java中字符使用单引号，字符串则使用双引号。
public class AList<Item> implements List61B<Item>{...}, implements, 接口继承，子类可以使用父类的方法，也可以覆盖父类的方法; AList将保证拥有并定义List61B接口中指定的所有属性和方法; AList is a List61B, 他们之间是is a关系; 在AList中实现List61B的方法时，@Override是必要的, 这是为了提醒编译器通知你可能发生的错误。
List61B<Item> lst = new AList<>();完成多态。
StdRandom库生成随机数文档。
assertEquals(message, expected, actual), JUnit测试失败时输出有用信息, 将预期值和实际值作为message。
Difference between implement and extends。
实现继承extends(is a关系, 继承…)关键字，子类继承父类的所有成员包括(构造函数不被继承)：
- 所有实例和静态变量
- 所有方法
- 所有嵌套类
在子类的构造函数中需要调用父类的构造函数，在子类的构造函数中使用super()关键字。原因: 比如TA extends Human(TA is a Human), 先需要创建一个人，接着创建TA才有意义; 当然如果我们不这样做，Java会自动调用super类的无参构造函数。
Java中的每个类都是Object Class或者是它的后代(descendant), 类没有显示地extends仍然会隐式地extends Object Class。
Java可以用interface(接口)类型来充当函数指针。
通过接口继承来定义一个比较接口CompareTo，解决Object对象之间不能比较的问题。
抽象数据类型(Abstract Data Type), 简称ADT, 指的是一种数据类型，只带有行为，没有任何具体的方式来实现展示这些行为(抽象的); java.util库中包含三个最重要的ADT: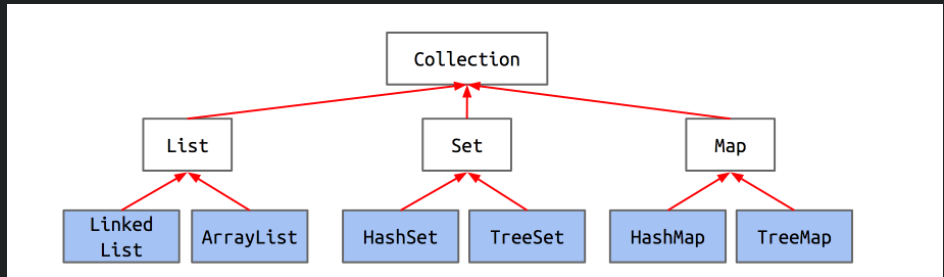
- List, 比较流行的实现是(ArrayList)List<String> lst = new ArrayList<String>();
- Set, 比较流行的实现是(HashSet)Set<String> ss = new HashSet<>();
- Map。比较流行的实现是(HashMap)Map<String, Integer> counts = new HashMap<String, Integer>();
接口(interface)的特性:
- 所有方法都必须是public
- 所有变量都必须是public static final，final类似于cpp的const
- 无法实例化
- 默认情况下，所有方法都是abstract的，除非指定为defualt
- 每个类可以Implements多个Interface。
抽象类(Abstract类似cpp), 介于interface和concrete class之间。
- 方法可以是public也可以是private，或者protected
- 可以有任何类型的变量
- 无法实例化
- 默认情况下，方法是concrete的，除非指定为abstract
- 每个类只能Implements一个Abstract
  1
  2
  3
  4
  5
  6
  public abstract class GraphicObject {
  public int x, y;
  public void meveTo(int newX, int newY) { ... }
  public abstract void draw();
  public abstract void resize();
  }
wrapper class(包装类)，如int的包装类是Integer。Java可以在原始类型和包装类型(也成为引用类型)之间进行隐式转换。两个方向的转换成为装箱(box)(int->Integer), 拆箱(unbox)(Integer->int); 注意:
- 数组永远不会自动装箱或自动拆箱
- 自动装箱和拆箱会对性能产生影响
- 包装类型比原始类型使用更多的内存, 关于内存使用信息的拓展此链接或链接
Java同如CPP这样的语言，会自动隐式向上类型转换，若占用字节较大的类型转换为较小的类型则需要手动去转换。
不可变数据类型，如String或加上final关键字修饰的基本类型。
- 优点：防止错误并使调试更容易
- 缺点：需要创建一个新对象才能更改属性。
在Java中异常是对象，抛出异常的格式throw new IllegalArgumentException("can't add null");
在Java中可以定义一个迭代器接口, 如ADT需使用则extend或者Implement这个接口，需要有next, hasNext方法。
1
2
3
4
public interface Iterator<T> {
boolean hasNext();
T next();
}

Java中创建Package(类似于cpp的namespace), 存储package的文件夹名称应该和包一致

package ug.joshh.animal;

public class Dog {
    private String name;
    private String breed;
    …
}

JAR文件就像zip文件一样，完全可以将文件解压缩并转换回.java文件。
public、protected、package-private、private的访问控制权限:
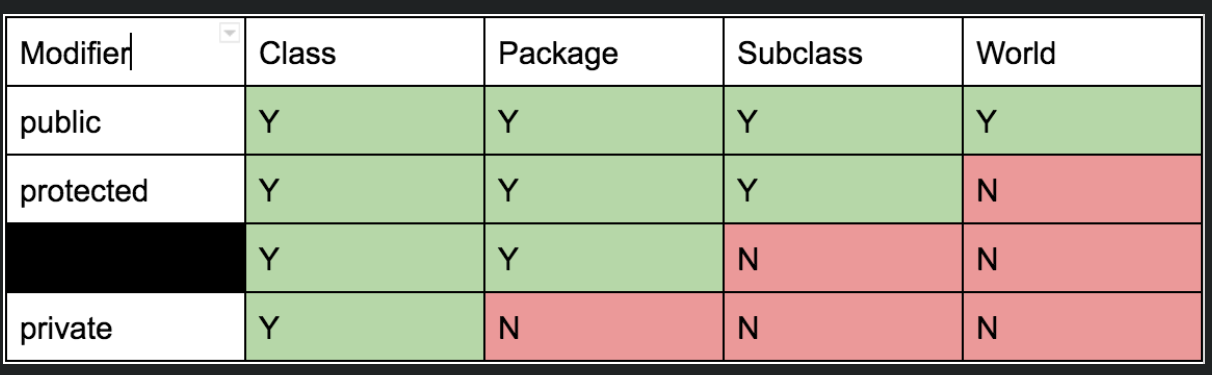
Java中操作文件，查看File javadocs和使用Utils.java类，该类具有许多有用的文件操作辅助函数。
序列化(seralize), 将java对象序列化为文件(持久性)，通过implementsSerializable接口

使用Utils类(proj Gitlet提供的子集)中的辅助函数来序列化和反序列化

Model m;
File outFile = new File(saveFileName);

// Serializing the Model object
writeObject(outFile, m);
// ----------------------------------
Model m;
File inFile = new File(saveFileName);

// Deserializing the Model object
m = readObject(inFile, Model.class);

可变参数形式static void writeContents(File file, Object... contents)
常用ADT的操作
- Stacks
  - push(int x): 将x放在栈顶
  - int pop(): 获取栈顶元素
- Lists
  - add(int i): 添加一个元素
  - int get(int i): 获取索引i处的元素
- Sets
  - add(int i): 添加一个元素
  - contains(int i): 返回集合是否包含值得布尔值
- Maps
  - put(K key, V value): 将键值放入哈希表中
  - V get(K key): 获取key对应得值
Java泛型bounded type parameter
Collection可以由许多不同的数据结构实例化

IDEA Skill

左键点击行号的右侧打断点
条件断点，在断点的基础上右键增加条件。进入Debug模式后，拖动console到右侧可以同时显示console和Debugger。
比较好用的Plugin: Java visualizer, IdeaVim, IDEA自带的Sheck Style。
Step into vs. Step over, Step into进入函数，而Step over则不进入函数直接向下执行。Step out跳出函数。
Resuming类似于continue，跳到条件断点的下一个条件，在step over的左下侧向右的绿色箭头
Destructive vs. Non-Destructive, 非破坏性调用函数没有修改传入的数据结构，相反破坏性则修改了传入的数据结构。
创建JAR文件
- File -> Project Structure -> Artifacts -> JAR -> “From modules with dependencies
IDEA将生成的.class文件存储在out或target文件夹中。

Algorithm

1.(Big-Theta$\Theta$来代替order of growth(增长级))

- Only consider the worst case.
- Pick a representative operation (aka: cost model)
- Ignore lower order terms
- Ignore multiplicative constants.

2.并查集

属性和方法

- Connect()
- isConnect()
- find()
- parent[]

优化

路径压缩
$$lg^n := \begin{cases}0, & \text {if n $\leq$ 1}\ 1+lg^(lgn), & \text{if n $>$ 1} \end{cases}$$

int find(int p) {
while (p != id[p]) {
        id[p] = id[id[p]]; // 路径压缩，使得下次查找更快
        p = id[p];
    }
    return p;
}

按秩合并

规则：将height较小的Set连接到height较大的Set

3.渐近线分析

并不是所有两层for循环的复杂度都为$\Theta(N^2)$, 比如下面这个for loop的复杂度为$C(N) = 1 + 2 + 4 + … + N = 2N-1$(如何N为2的幂)

public static void printParty(int N) {
    for (int i = 1; i <= N; i = i * 2) {
        for (int j = 0; j < i; j += 1) {
            System.out.println("hello");   
            int ZUG = 1 + 1;
        }
    }
}

递归, 复杂度为$C(N) = 1 + 2 + 4 + 8 + … + 2^{N-1} = 2(2^{N-1})-1 = 2^N-1 = \Theta(N)$

public static int f3(int n) {
    if (n <= 1) 
        return 1;
    return f3(n-1) + f3(n-1);
}

$O$(Big O)是$\Theta$(Big Theta)在不考虑最好情况和最坏情况下的表示, 在不同的输入，运行时间不同的情况下，它允许我们做出没有实例(case)限定的简单语句

$\Theta$形式表示增长级(Order of growth)为$F(N)$
$\Omega$表示增长级小于等于$F(N)$
$\Omicron$表示增长级大于等于$F(N)$
4.归并排序(Merge Sort)
结合选择排序来理解，在选择排序上进行优化$\Theta(nlogn)$, 额外开辟一个存储结果的空间，利用双指针获得最后的排序数组。

5.均摊(Amortized)分析

$\Phi_i = \Phi_{i-1} + a_i - c_i$, 其中$c_i$是操作的真实开销，$a_i$是随机摊销操作的开销，在所有$i$中必须一致。假设$\Phi_0 = 0$。

6.二叉搜索树(BST Binary Search Trees)

除了含有二叉树的属性外，对于树中的每个节点X，要求左子树中的每个键都小于X的键，右子树中的每个键都大于X的键。需要成员为root, 具备的私有内嵌类有BSTNode，其中的成员为key, value, left, right, node count。

插入`put`

总是在叶节点插入, 递归找到null节点后创建一个node count为1的Node。
删除
被删除节点没有子节点, 直接删除它的父指针
被删除节点有1个子节点，将父节点的子指针分配给被删除节点的子节点
被删除节点有2个子节点，由新的节点来替换，必须要大于左子树，且小于右子树, 即取右子树的min或者左子树的max两种解决方案。Hibbard deletion，维护好删除节点后后BST的平衡性, 要实现的方法有ceiling, floor, deleteMin, deleteMax。
注意
get递归返回值，而put递归返回一个子树。
属性
depth, height, average depth:

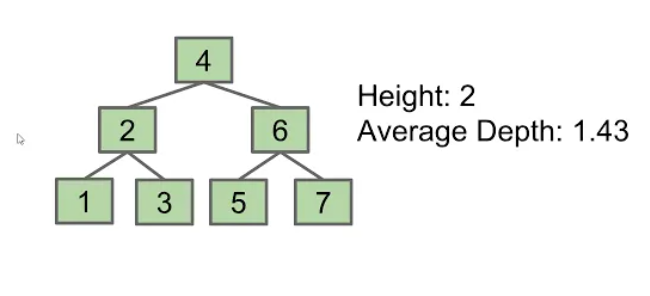
$$Average Depth = \frac{\sum^D_{i=0}d_in_i}{N}$$
其中$d_i$为depth, $n_i$为当前层节点的数目

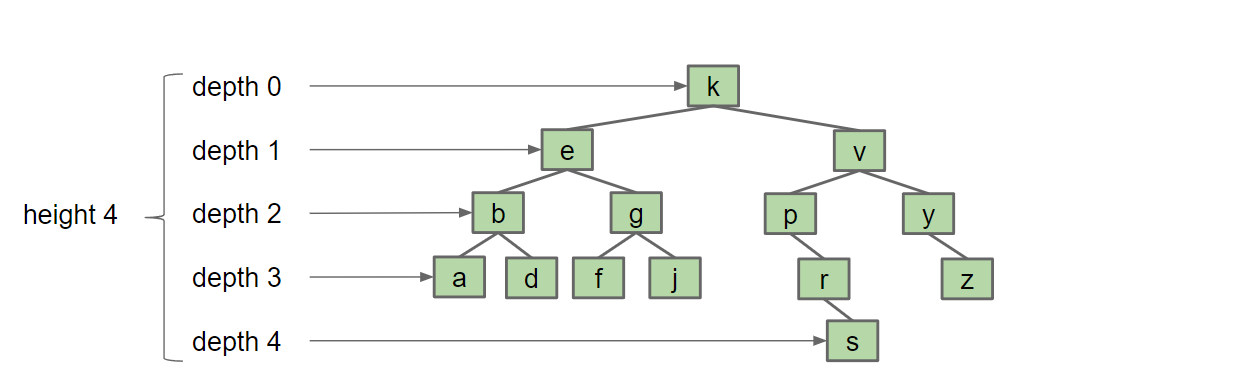
BST存在的问题
我们总是在叶子节点处插入，这是导致高度增加的原因。插入顺序不同会导致高度不同。
树的高度决定了最坏情况的运行时间，
树的平均深度决定了平均情况的运行时间。
7.B树(B-Trees)
B树很好地避免了BST存在的问题, 最糟糕搜索情况为$O(N)$——以链表的形式展开
BigO $\not =$ Worst Case
L非常大的情况，在数据库和文件系统中会出现。
2-3树, 通常指明L(每个节点中项(item)的最大数量)为2，而2-3指的是可以拥有的孩子节点的数量为2或3。
max-degree指的是所能拥有最多孩子节点的个数, B树可视化模拟。
B树不变量(Invariant)
保证了B树的bushy。
所有叶子节点到根节点有着相同的距离
含有k项的节点一定含有k+1个子节点。
B树的插入
向叶子节点中插入，沿着树向下遍历以及根据当前节点项的大小左右遍历
将节点添加到叶子节点后，如果项数>L, 则弹出中左(middle left)项，加入到父节点中重新排列。
如果父节点的项数也大于L，则再次弹出中左项目
重复完成此过程，直到父节点可以容纳或到达根节点。
搜索B树运行时最坏情况分析
总运行时间$O(LlogN)$, 搜索在树中最大的数，遍历到底部需要$O(logN)$, 向右遍历得到最大数需要$O(L)$, 因为当前节点有有L个项。
B树的删除
分以下几种情况, 打算做到15445的proj2 B+Tree的时候再review B树删除操作的slide
Case 1: Multi-Key Sibling
Case 2: Multi-Key Parent
Case 3: Single-Key Parent and Sibling
B树的特性总结
Nodes may contain between1andLitems.
contains works almost exactly like a normal BST.
add works by adding items to existing leaf nodes.
If nodes are too full, they split.
Resulting tree has perfect balance. Runtime for operations is $O(logN)$.
B-trees are more complex, but they can efficiently handle ANY insertion order.
B树实现起来比较复杂，相对来说比较慢
8. 红黑树(Red-Black Trees)
left-Leaning Red Black Binary Search Tree (LLRB)
属性
不存在节点含有两个red links(意味着4个item一个节点，在2-3树中是不存在的)。
叶子节点到root的black links数一致。
规则
在2-3树，插入时总是使用red links。
通过旋转使得red links在左侧。右侧的Red links是不允许的, 除了temporary 4 node即含有两个red links的子节点
如果出现2个连续的左侧连接，则通过右旋转来调整为temporary 4 node
含有temporary 4 node, 即含有两个red links的子节点, 则color clip来模拟BST的split. Color Flip指将当前节点的两个red links变黑，并将父节点的black links变红。如果当前节点为根节点则，则不存在将父节点变红这一步。
红黑树总结
61B的demo通过insert来理解红黑树的特性。
红黑树和B树的复杂度一致
将BST转化为红黑树的代码实现

9. 哈希

Properties of HashCode(哈希值)
- 必须是整数
- .hashCode()在同一对象上运行两次，应该返回相同的数字
- 被考虑的两个对象.equal()必须具有相同的哈希码
实际上哈希表key-value对，在Java中key在哈希表中的索引是由hashCode()成员函数生成的。
溢出会引起冲突(出现在哈希值过大的情况下)，比如最大的整型数加1会变成最小的整型数
避免冲突的方式，取模而不是无限地增大空间。
尝试用链表数组(ArrayList), 即数组元素为链表，来作为哈希的空间，处理碰撞的复杂度$\Theta(Q)$, 因为add和contains需要检查当前链表数组元素(即链表)的第Q项是否为存在。最坏的情况下为所有项目的hashCode都是相同的，因此需要$\Theta(N)$。
利用模运算来减少bucket的数量了。
动态增长哈希表
假设含有M个Bucket和N个items。Bucket相当于一个链表数组的一个元素。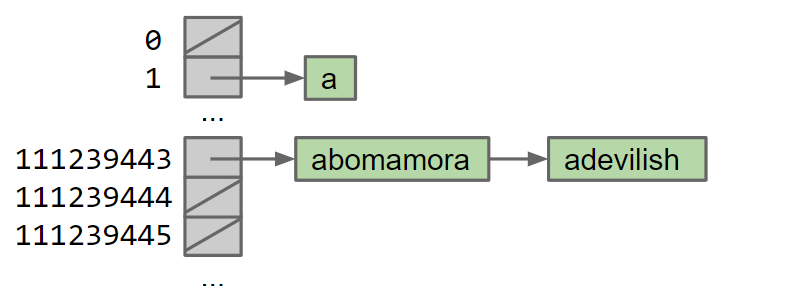
每隔一段时间就Double M创建一个新的哈希表，来确保时间复杂度为$\Theta(N/M)$即$\Theta(1)$。
遍历旧的哈希表，将元素一个个地添加到新的哈希表中。因为哈希表大小的改变，元素对哈希表大小的模数也会发生变化。
Load Factor(即N/M)等于上述最好情况(Best case)的运行时间。如果N在增加，Load Factor也将会持续增加
Load Factor Threshold，当Load factor大于load factor threshold时就resize。 resize需要$\Theta(N)$的时间，因为需要将N个items添加到哈希表中，每个添加需要$\Theta(1)$的时间。
注意: 当resize时，不需要检查项目是否已经存在于Linkedlist中(因为知道没有重复项)，所以Add只需要$\Theta(1)$的时间
经验法则
使用base策略，即模数。
使用一个小的质数作为base。素数非偶特性有助于避免溢出问题，以及更容易计算等等。
注意
当一个目标变量改变，它的哈希值也改变。因此不要再哈希表中存储能够改变的Objects
避免冲突的方法
开放定址法(open addressing), 如果目标bucket已经存在，则选择不同的bucket
- linear Probing(线性探测法)，如果当前bucket已被占用，使用下一个bucket，一个接着一个扫描

10. 堆和优先队列

涉及到搜索树的优先级?
堆的数据结构是二叉搜索树

最小堆

属性
- 每个节点都小于等于它的两个子节点。
操作
- add: 临时添加到堆尾，swimming到合适的位置。
- getSmallest: 返回堆的根。
- removeSmallest: 将堆中的最后一项交换到根中，将层次结构下沉到适当的位置。
  Implementation of PQ
leftchild(k) = k * 2;
rightchild(k) = k * 2 - 1;
parent(k) = k / 2;
实现基于的数据结构: 数组, BST, 哈希表，堆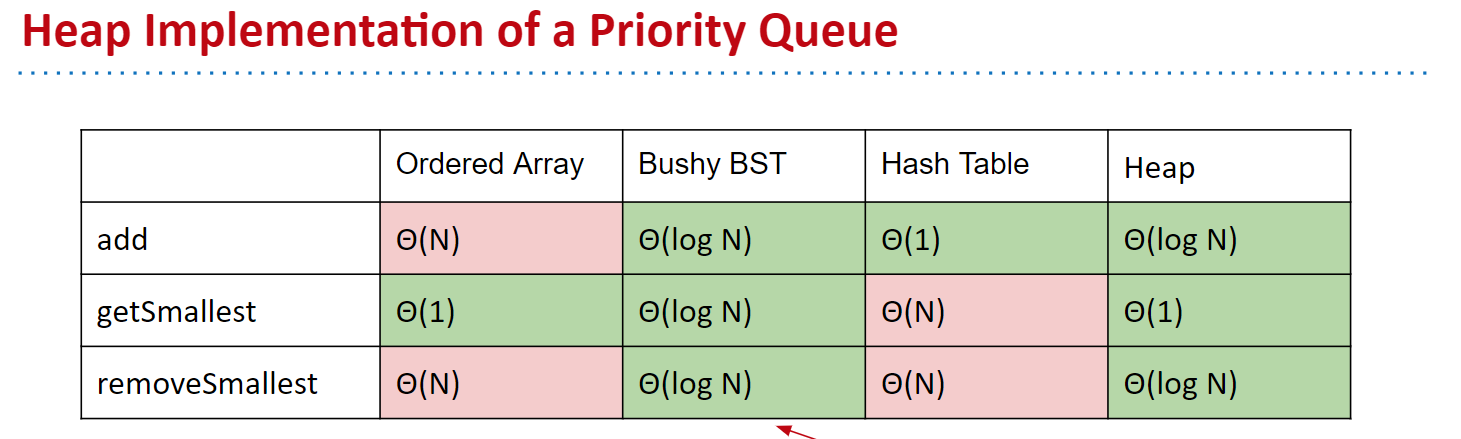

树和图的遍历

树也是图的一种实现方式, 无环。
先序遍历(preorder traversal)适合打印目录结构。
后序遍历(postorder traversal)同样适用计算出当前目录下的文件总大小。

简单图的定义

不存在一个顶点的边回到自身。
不存在两条边连着同样的顶点。

图的类型

Acyclic(非循环) vs. cyclic(循环), 循环指的是第一个顶点和最后一个顶点是同一个。
Directed(有向) vs. Indirected(无向)
With edge label(a.k.a. weight)(边权重).

图的问题

s-t Path? 由顶点s到t是否存在路径?
Connectivity? 每个顶点到其它顶点是否存在路径?
Biconnectivity? 如果将某两个顶点的边移除，图就不是连通的了。
Shortest s-t Path?
Cycle Detection?
Euler(欧拉) Tour? 是否存在一个cycle使得所有边只使用一次。
Hamilton Tour? 是否存在一个cycle使得所有顶点只使用一次。
Planarity(平面化)? 能否画一张图不出现交叉的边。
Isomorphism? 两个图是否为同构?

Depth-First Traversal

marks, 可以避免connected(v, t)–(寻找neighborhood)的无限循环。
marked(), 判断是否被标记
edgeTo[w] = v, 添加边

Graph Traversal

Dfs postorder, 若当前顶点的邻居都被标记时才返回当前顶点的值。
Dfs preorder, 若遍历到当前顶点即打印值。
BFS

Graph API

public class Graph {
  public Graph(int V):               Create empty graph with v vertices
  public void addEdge(int v, int w): add an edge v-w
  Iterable<Integer> adj(int v):      vertices adjacent to v
  int V():                           number of vertices
  int E():                           number of edges

图的实现

邻接矩阵(无向图)
邻接链表(有向图)
边集合, 如{{0, 2}, {0, 1}}表示顶点0分别指向1和2。

CS61B Data Structure Notes

Java Syntax

IDEA Skill

Algorithm

1.(Big-Theta$\Theta$来代替order of growth(增长级))

2.并查集

属性和方法

优化

3.渐近线分析

4.归并排序(Merge Sort)

5.均摊(Amortized)分析

6.二叉搜索树(BST Binary Search Trees)

插入put

删除

注意

属性

BST存在的问题

7.B树(B-Trees)

B树不变量(Invariant)

B树的插入

搜索B树运行时最坏情况分析

B树的删除

B树的特性总结

8. 红黑树(Red-Black Trees)

属性

规则

红黑树总结